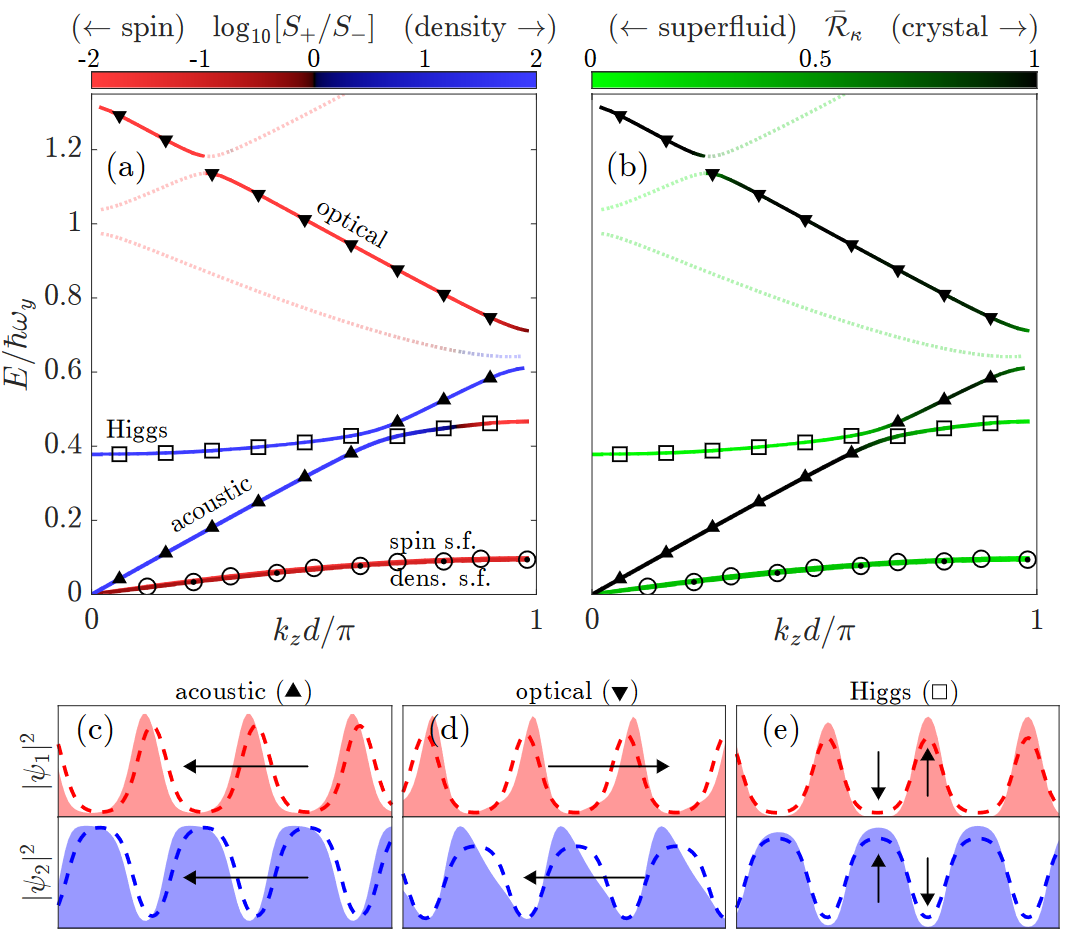
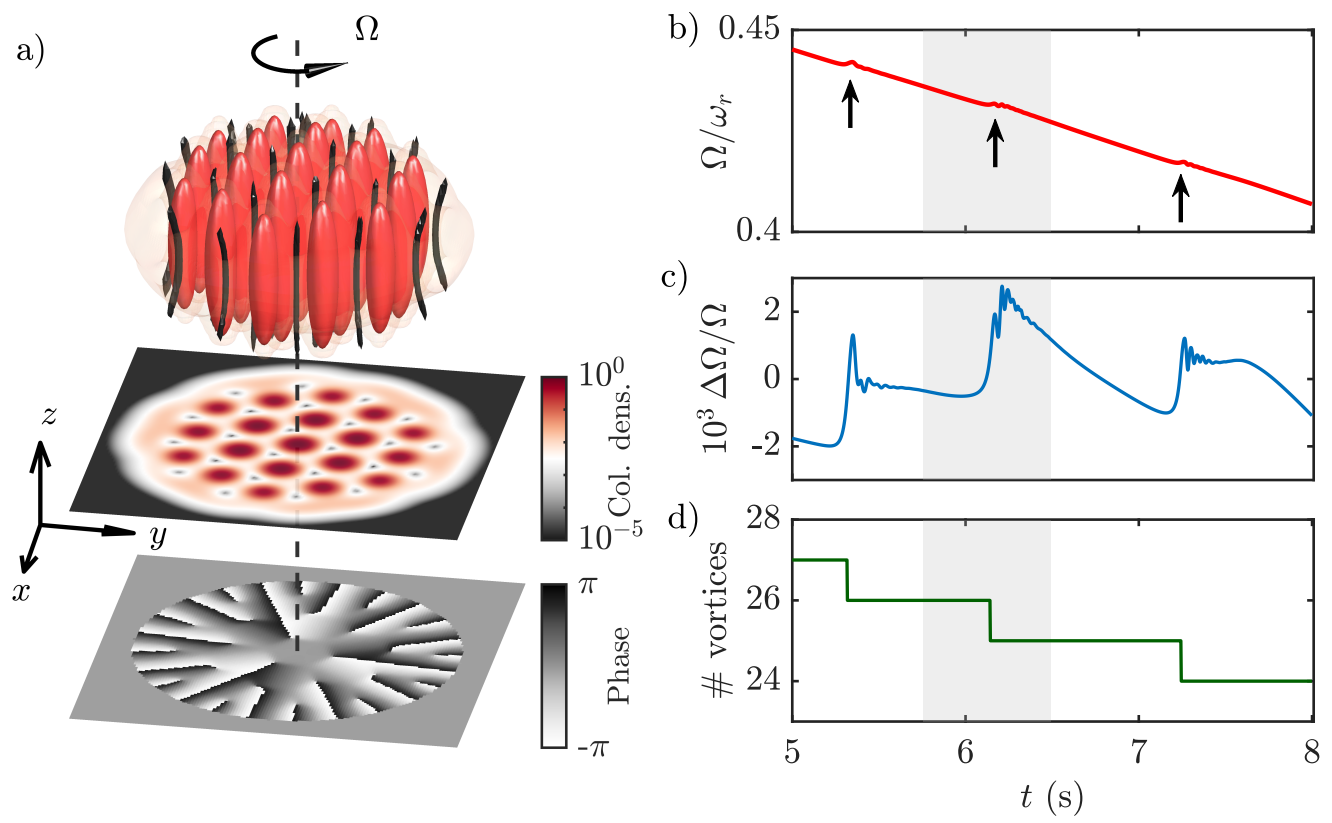
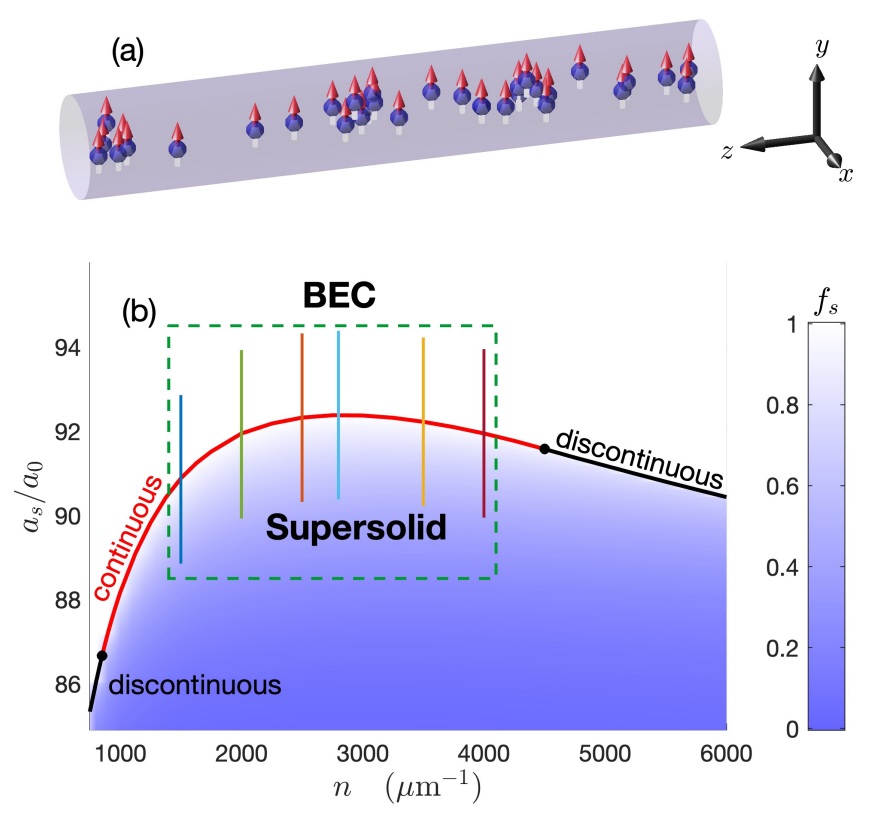
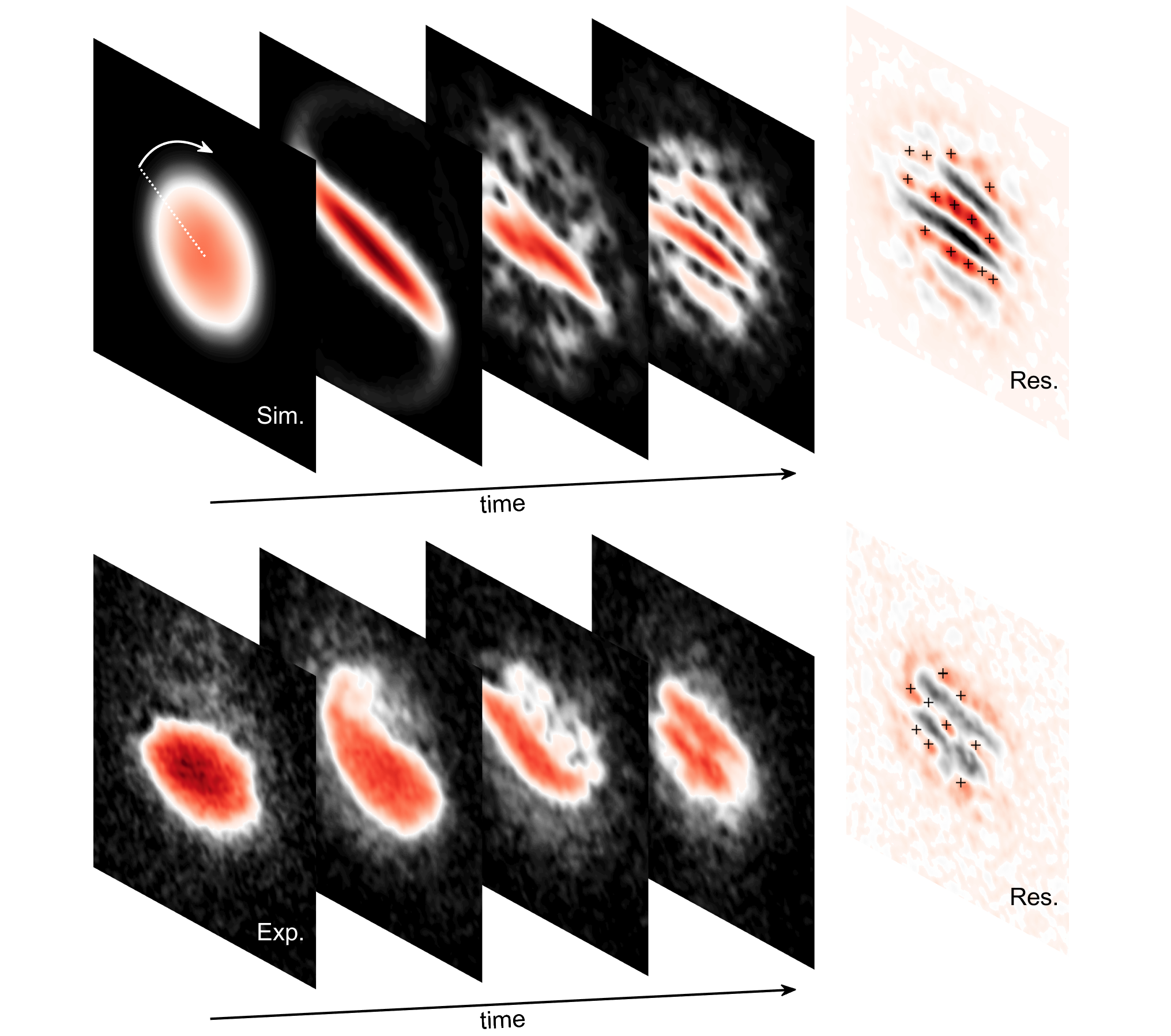
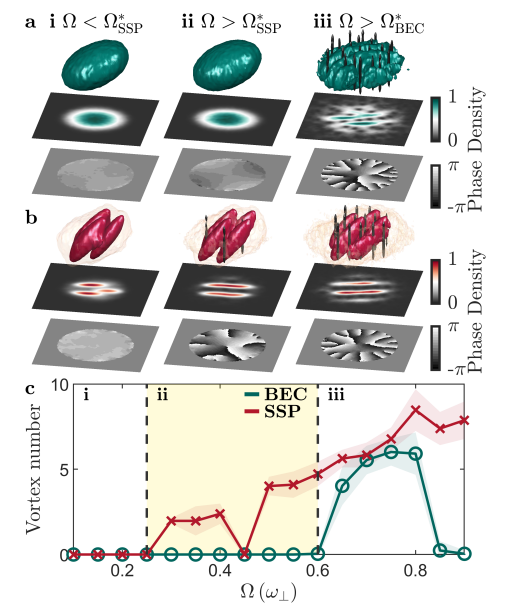
 In an internal collaboration between the Er-Dy Lab and the Theory subgroup, our new pre-print reveals a fundamental difference in vortex nucleation between the unmodulated superfluid and the modulated 2D supersolid phase of dipolar BECs. This work builds on our previous investigation of vortices in dipolar gases (see our writeups here and here) and of supersolids with two-dimensional crystalline order (see our writeup here). This opens the door to study the hydrodynamic properties of exotic quantum systems with multiple spontaneously broken symmetries, ranging from quantum crystals to neutron stars — for a general overview of the connection between glitches in the supersolid and neutron stars, see our writeup here.
In an internal collaboration between the Er-Dy Lab and the Theory subgroup, our new pre-print reveals a fundamental difference in vortex nucleation between the unmodulated superfluid and the modulated 2D supersolid phase of dipolar BECs. This work builds on our previous investigation of vortices in dipolar gases (see our writeups here and here) and of supersolids with two-dimensional crystalline order (see our writeup here). This opens the door to study the hydrodynamic properties of exotic quantum systems with multiple spontaneously broken symmetries, ranging from quantum crystals to neutron stars — for a general overview of the connection between glitches in the supersolid and neutron stars, see our writeup here.
See the pre-print here: arXiv:2403.18510.

 If you have been searching for a high-level overview of the dipolar supersolid phase, look no further than this open access article by
If you have been searching for a high-level overview of the dipolar supersolid phase, look no further than this open access article by